علی کرمی 
چگونه از نظریه بازی‌ها در بازاریابی محصول خود بهره ببریم؟
نگاه برخی از افراد به بازاریابی و مارکتینگ، نگاه حرفه‌ای و شغلی آن‌هاست. برخی دیگر از افراد، مانند مدیران و سهام‌داران شرکت‌ها، به بازاریابی به‌عنوان وسیله رشد و پیشرفت نگاه می‌کنند. اما اگر بخواهیم نگاه کلی به این مبحث داشته باشیم، می‌توانیم بازاریابی را به‌عنوان یک بازی در نظر بگیریم. به‌طرز جالبی، مارکتینگ نزدیکی بسیار
نگاه برخی از افراد به بازاریابی و مارکتینگ، نگاه حرفه‌ای و شغلی آن‌هاست. برخی دیگر از افراد، مانند مدیران و سهام‌داران شرکت‌ها، به بازاریابی به‌عنوان وسیله رشد و پیشرفت نگاه می‌کنند. اما اگر بخواهیم نگاه کلی به این مبحث داشته باشیم، می‌توانیم بازاریابی را به‌عنوان یک بازی در نظر بگیریم.
به‌طرز جالبی، مارکتینگ نزدیکی بسیار خوبی با نظریه بازی‌ها دارد؛ در کل بازی تعدادی استراتژی، محیط بازی، بازیگر، اهداف و پاداش وجود دارد. همچنین در این بازی، گاهی برندگان و بازندگان وجود داشته و گاهی همه افراد نتیجه خوبی کسب می‌کنند. اگر با نظریه بازی‌ها آشنا باشید، قطعا شباهت موجود را احساس می‌کنید.
همانند هر بازی دیگری، اگر شما بتوانید قواعد را به‌خوبی درک کنید، توانایی شکست دیگران را پیدا کرده و در نهایت می‌توانید به موفقیت دست یابید. در این مقاله، با ذکر یک مثال و توضیح مفاهیم جزئی نظریه بازی‌ها، قصد داریم ابعاد مختلف بازی بازاریابی را بررسی کرده و توسط این نکته به یک برتری نسبی در کسبوکار برسیم.
تاریخچه نظریه بازی‌ها
در سال ۱۹۲۰ جان ون نیومن، ریاضی‌دان سرشناس، شروع به تفکر راجع به ضعف خود در کارت‌بازی کرد. پس از مدت زیادی بررسی، وی به این نتیجه رسید که دلیل عدم موفقیت وی، تمرکز بر روی کارت‌ها به‌جای تمرکز بر روی طرف مقابل است؛ این ایده باعث شد تا وی برای حل این مشکل، تئوری جدیدی مطرح کند.
وی در سال ۱۹۴۴ با یک اقتصاددان به نام اسکار مورگن‌استرن همراه شد تا تئوری بازی‌ها و رفتارهای اقتصادی را مطرح کند. این کتاب آن‌قدر مهم بود که روی جلد مجله نیویورک تایمز در آن زمان چاپ شد، اتفاقی که پیش از آن تنها برای انیشتین و نظریه نسبیت وی رخ داده بود.
نیومن و مورگن‌استرن ثابت کردند که در یک بازی جمع صفر (بازی که نفع یک بازیگر به ضرر دیگری تمام می‌شود)، یک راه‌حل و استراتژی بهینه وجود خواهد داشت. در آن زمان، چنین اثباتی یک اتفاق مهم و تاثیرگذار در مباحث اقتصاد و استراتژی جنگی محسوب می‌شد.
با این وجود، بیشتر سناریو‌های بازی در زندگی روزمره یک درگیری خالص نیستند؛ یعنی لزوما افراد برای تصمیم‌گیری با یکدیگر مقابله کامل ندارند. در اغلب اوقات، ما برای دریافت منفعت مشترک با یکدیگر در ارتباطیم. شش سال پس از این اتفاق، مشکل بازیهای جمع صفر توسط جان نش حل شد.
تعادل نش
تعادل نش در یک بازی زمانی رخ داده است که اگر شما قصد عوض کردن انتخاب (استراتژی) خود را داشته باشید، نتوانید نتیجه (مطلوبیت) بیشتری را با توجه به انتخاب طرف مقابل، به دست آورید. نش اثبات کرد که برای هر بازی غیر جمع صفر، حداقل یک راه‌حل وجود دارد.
این نکته تاثیر بسیار وسیعی بر روی تفکر نسبت به استراتژی‌های رقابتی داشت. با توجه به این بحث، بازی‌ها دیگر تنها وابسته به قدرت و اراده بازیکنان نبودند؛ بلکه برای موفقیت، ترکیبی از همکاری (ضمنی و غیر ضمنی) و رقابت لازم بود.
همچنین لازم به ذکر است که تعادل‌های نش نه‌تنها پایدار هستند، بلکه خود تقویت‌کننده نیز محسوب می‌شوند. هرزمانی که یک تعادل پایدار نش شکل بگیرد، تغییر وضعیت علاوه بر پرهزینه بودن، دشوار هم خواهد بود؛ حتی در برخی از موارد، مانند بازی دوراهی زندانیان، تغییر تعادل بازی به نتایج منفی برای هر دو طرف ختم می‌شود.
یک مثال در بازاریابی: بودجه رقابتی
برای اینکه درک بهتری از تعادل نش در سناریو‌های دنیای واقعی و بازاریابی داشته باشیم، بهتر است به مثال زیر بپردازیم.
فرض کنید که در یک بازار، دو بازیکن رقابتی قصد دارند بودجه تبلیغات خود را مشخص کنند. در نقطه ابتدایی بازی، هر دو بازیکن به سود و بودجه یکسانی دسترسی دارند.
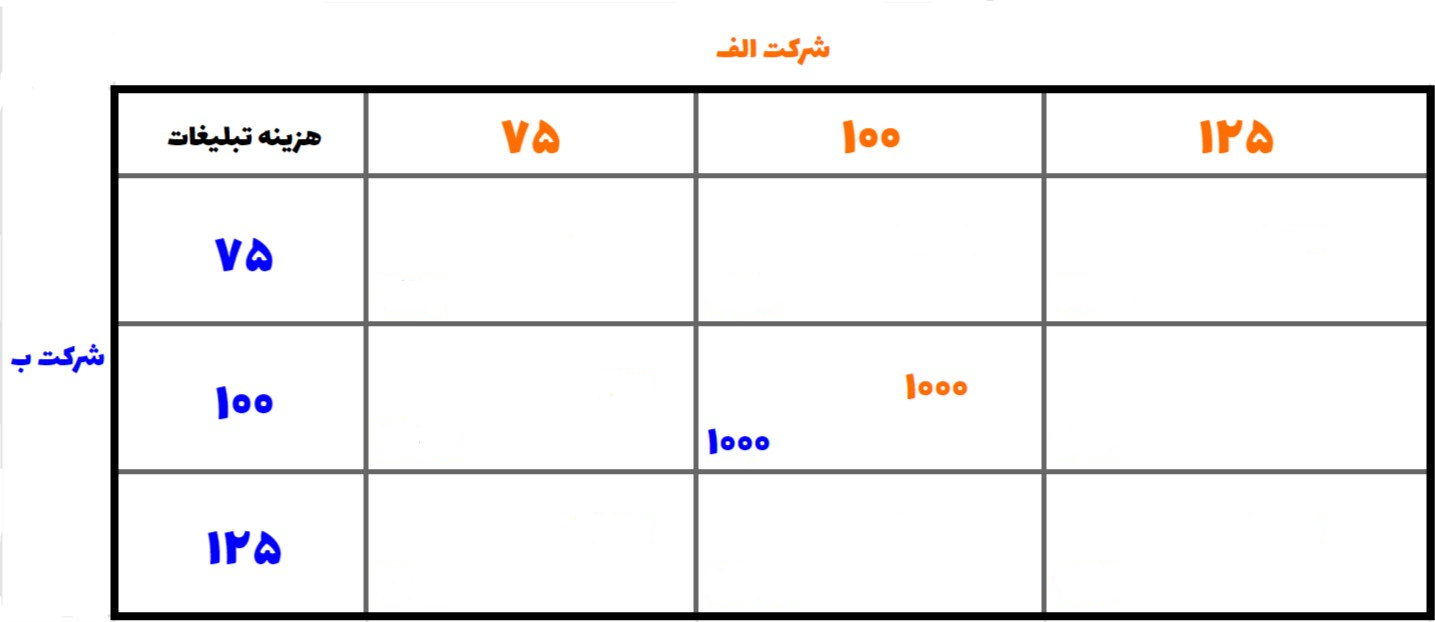
در این بازی فرض می‌کنیم که هرکدام از بازیکنان، غیر از وضعیت اولیه، توانایی انتخاب دو گزینه دیگر را دارند:
- شرکت هزینه تبلیغات خود را افزایش داده تا برند وی شناخته‌تر شود و به فروش بیشتری دست یابد.
- شرکت هزینه تبلیغاتش را کاهش داده تا آن مبلغ را صرف ارائه تخفیف بر روی محصولاتش کند، تا از این طریق نیز به فروش بیشتری دست یابد.
هر دو این تصمیمات (Action) هزینه‌ها و منفعت‌های خودشان را دارند. همچنین اینکه در این مثال، ما فرض می‌کنیم هر مبلغی که صرف تبلیغات نشده به ارائه دادن تخفیف روی محصولات اختصاص پیدا می‌کند.
همان طور که خواهیم دید، میزان اثرگذاری هرکدام از استراتژی‌های یک بازیکن به استراتژی بازیکن دیگر وابسته است. به همین دلیل، هیچ‌کدام از بازیکنان از میزان اثرگذاری تصمیمات خود باخبر نمی‌شوند؛ تا زمانی که بازی در بازار به‌طور کامل رخ دهد.
در اینجا، جدول بازی را به همراه سود (مطلوبیت یا پاداش) رسم کرده‌ایم:
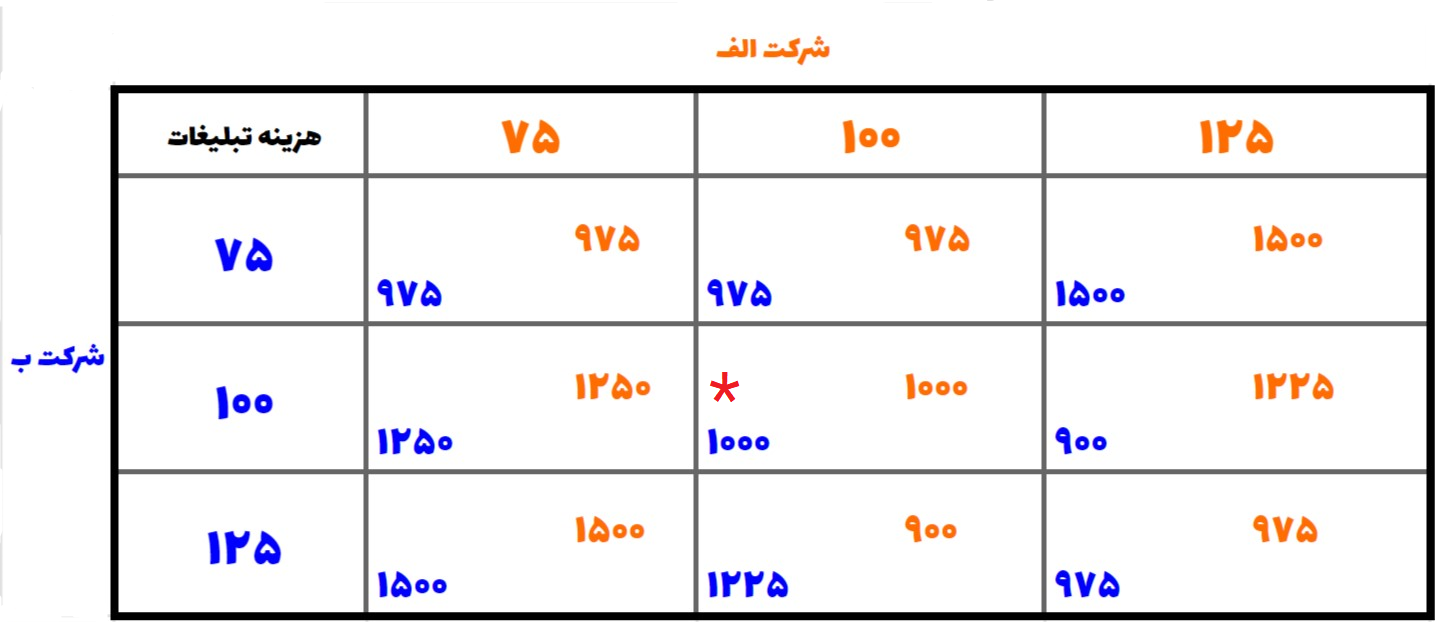
هزینه تبلیغات در جدول استراتژی‌های هر شرکت محسوب می‌شوند. هرکدام از ۹ خروجی بازی نیز در جدول نوشته شده‌اند؛ اعداد نارنجی سود شرکت الف در آن سناریو بوده و اعداد آبی، سود شرکت ب در همان سناریو هستند.
همان طور که می‌بینید، حتی یک مثال به این سادگی نیز به یک ماتریس پیچیده برای پاداش‌ها ختم می‌شود. به‌عبارت دیگر، صرفا اتخاذ تصمیم برای تبلیغ کردن یا تخفیف دادن، اطلاعات زیادی راجع به پاداش نهایی به ما نخواهد داد؛ و اینکه تنها از تصمیم خود، نتیجه خود را نمی‌توانیم پیش‌بینی کنیم.
اما اگر در این مثال به دنبال تعادل نش بگردیم، تصمیمات درست به‌راحتی نمایان می‌شوند.
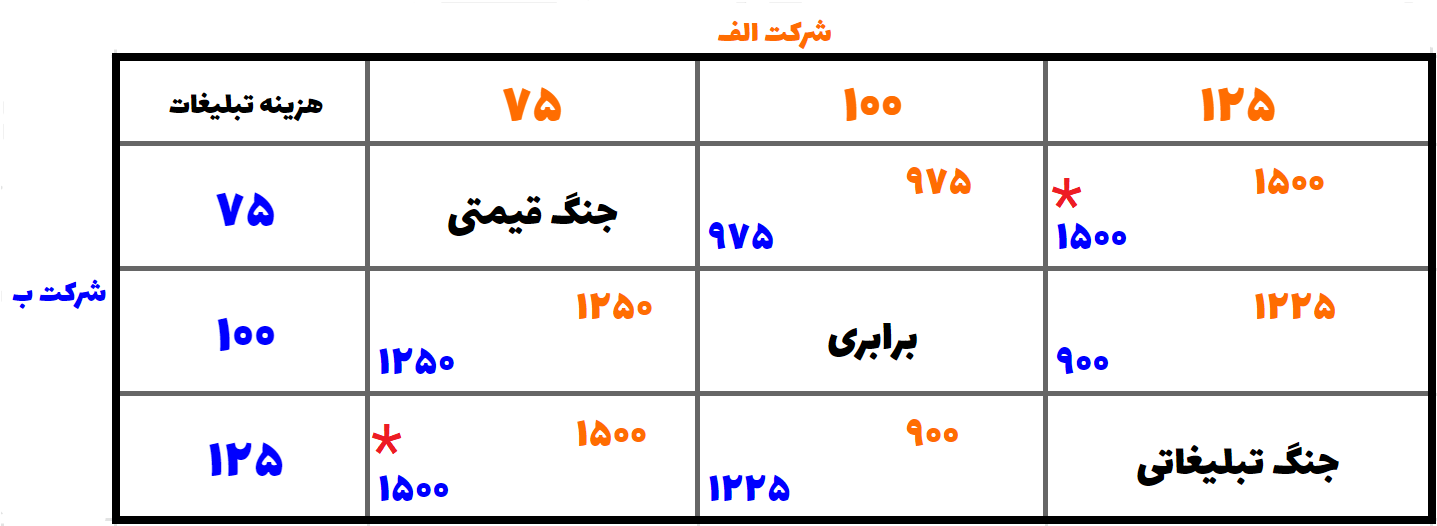
ستاره قرمز نشانه سناریوی تعادل نش است.
با کمی دقت به پاداش‌های سناریو‌های ممکن، می‌بینیم که اکثر آن‌ها ناپایدارند؛ به این معنی که یک بازیکن می‌تواند با تغییر استراتژی خود به نتیجه مناسب‌تری دست پیدا کند.
اگر هر دو بازیکنان تصمیم به افزایش بودجه تبلیغاتی خود بگیرند، آن‌ها گرفتار یک جنگ تبلیغاتی پایدار شده و همچنین اگر هر دو به سراغ استراتژی تخفیف بروند نیز به جنگ قیمتی دچار می‌شوند. پیش نگرفتن هیچ استراتژی جدید نیز یک بن‌بست محسوب می‌شود؛ چرا که برای هر دو بازیکنان امکان کسب سود بیشتر وجود دارد.
با این حال، اگر بازیکنان استراتژی‌های خلاف یکدیگر را پیش بگیرند (جداول پایین سمت چپ و بالا سمت راست)، هر دو آن‌ها به سود حداکثری در این بازی خواهند رسید. در این بازی دو تعادل نش وجود دارد چرا که در هر دو این پیامد‌ها، پاداش بازیکن ثابت بوده و تنها استراتژی‌های آن‌هاست که متفاوت است.
این مثال تا حدی می‌تواند نماینده اتفاقات در دنیای واقعی باشد. باوجود اینکه تعادل در بازار در مواقع بسیار کمی توسط تنها یک حرکت رخ می‌دهد، اما بازارها بالاخره دسته‌بندی شده و به پایداری (هرچند کوتاه‌مدت) می‌رسند. همچنین اینکه در زمان رسیدن به نقطه پایدار، شیفت و تغییر بازار به حالت دیگر بسیار دشوار بوده و هزینه زیادی را می‌طلبد: یک برند خاص و متفاوت که تصمیم به پایین آوردن قیمت‌ها گرفته یا یک برند تخفیف ده و ارزان که قصد کسب سود بالاتری دارد؛ هر دو آن‌ها مسیر سخت و پرهزینه‌ای پیش‌رو دارند.
بازیهای چند نفره
بدیهی است که بازارها تنها شامل دو بازیگر نیستند، و از تعداد زیادی بازیکن مختلف تشکیل می‌شوند. در نظریه بازی‌ها، این نوع شرایط بازیهای n-نفره نام دارند و به‌طور معمول، بر روی ائتلاف‌ها بنا می‌شوند.
برای این حالت، مثالی را بررسی می‌کنیم که در آن دو بازیگر تخفیف‌دهنده، دو برند متمایز و جریان ثابتی از رفت‌و‌آمد بازیگران جدید وجود دارد.
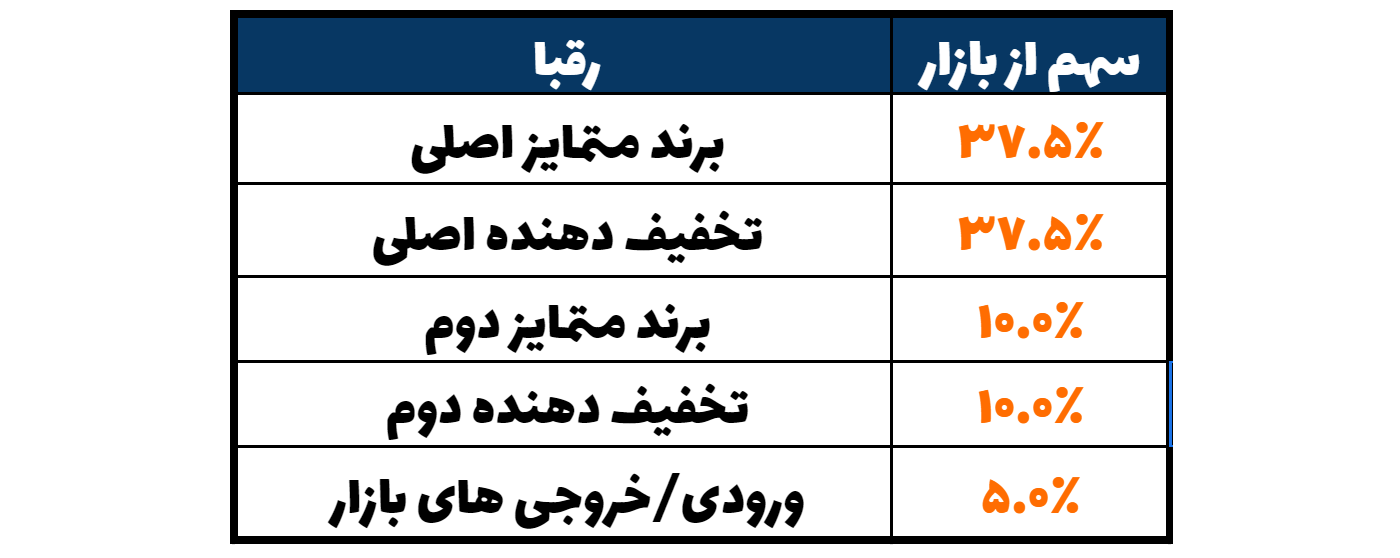
همان طور که می‌بینیم، دو ائتلاف طبیعی وجود دارد، اما هیچ‌کدام از آن‌ها غالب نیستند. اگر یک ائتلاف قصد داشته باشد تا روند و مسیر بازار را به دست بگیرد، باید ابتدا بازیگران کوچک‌تر را وارد گروه خودش کند.
نکته جالبی که اینجا وجود دارد، این است که سهم بازار شرکت‌ها تاثیر چندانی بر اثرگذاری آن‌ها ندارد؛ تنها چیزی که در این بازی تعیین‌کننده است، احتمال دادن رای ۵۱ام است. و در این مثال، شانس در اختیار داشتن این رای برای تمامی بازیکنان یکسان محسوب می‌شود.
همانند مثال قبلی، با وجود اینکه در حال بررسی مثال ساده‌ای هستیم، نتایج حاصل از این بازی اطلاعات بسیاری مهمی را در ارتباط با دنیای واقعی در اختیار ما قرار می‌دهند. یک مثال بسیار معروف این بازی، رقابت سونی و JVC در کنترل بازار نوارهای ویدیویی بود.
احتمالا شما نامی از «بتامکس» نشنیده‌اید؛ این استاندارد ویدیویی که هم‌زمان با VHS به بازار عرض شد، از لحاظ فنی کیفیت بهتری نسبت به VHS داشت. اما در هنگام عرضه توسط JVC شکست خورد، زیرا ائتلاف تشکیل‌شده از بازیکنان کوچک‌تر توسط JVC، قدرت بیشتری را به آن‌ها نسبت به سونی در اختیار قرار داد.
در بسیاری از موارد، دیده شدن به‌عنوان قوی‌ترین بازیکن می‌تواند یک ضعف رقابتی محسوب شود؛ چراکه این ویژگی تمامی بازیکنان دیگر را به ایجاد یک ائتلاف متقابل تشویق می‌کند.
چگونه از نظریه بازی‌ها بهره ببریم؟
در واقعیت، اجرا و بهره‌برداری از نظریه بازی‌ها بسیار دشوار است، چراکه تنها در مواقع نادری از ارزش‌ها و پاداش‌های نهایی باخبریم.
با این وجود، درک این نظریه به ما کمک می‌کند تا نیروها و عوامل موثر در کسبوکار خود را بهتر درک کنیم. همچنین تفکر به این شکل ما را مجبور کرده تا افکار منظم‌تری داشته و با رعایت قوانین بازی، به نتایج غافل‌گیر کننده‌ای برسیم؛ چرا که در مدل‌سازی‌های بازی از بسیاری سوگیری‌های خود فاصله می‌گیریم.
نویسنده: گرگ ساتل (Greg Satell)
مترجم: علی کرمی
عنوان اصلی مقاله: A Marketer's Guide to Game Theory
نشریه: DigitalTonto
نظرات