ول‌گردی در بازار و نظریه قدم‌زدن تصادفی

ولگشت، پرسه‌زنی، قدم‌زدن تصادفی یا random walk نظریه‌ای است که می‌کوشد حرکت تصادفی یک شیئ را توصیف کند. این موجودِ «قدم‌زن» می‌تواند هرچیزی باشد. کامپیوتری که به طور تصادفی به صفحات وب سر می‌زند، بچه‌ای که در پارک بین وسایل بازی جست‌وخیز می‌کند یا قیمت سهام که در بازار بالاوپایین می‌رود.

واضح است که با دانستن سابقه رفتار موجودی تصادفی به طور قطع نمی‌توان حرکت بعدی آن را پیش‌بینی کرد. اما موضوع جالب قاعده‌مند کردن همین رفتار پیش‌بینی‌ناپذیر است. درک درست از قواعد پرسه‌های تصادفی بی‌اندازه در درک صحیح بازار (چه بازار آهن باشد و چه بازار سهام) مفید خواهید بود. پس اگر قصد دارید به تجارت بپردازید، از الگوریتم جستجوهای گوگل سر در بیاورید یا در پارک به دنبال فرزند خود بگردید، آگاهی از نظریه قدم‌زدن تصادفی بی‌فایده نیست.

یک قدم رو‌ به جلو

هزار کودک در یک صف ایستاده‌اند. برای هر کدام از آن‌ها یک سکه می‌اندازیم. اگر شیر آمد کودک یک قدم به سمت راست می‌رود و اگر خط آمد کودک یک قدم به سمت چپ حرکت می‌کند. سکه کاملا سالم است و احتمال این‌که شیر یا خط بیاید برابر است با 50 درصد.

اگر برای هر کودک یک‌بار سکه بیندازیم، به احتمال زیاد در پایان آزمایش نیمی از کودکان یک قدم به سمت راست می‌روند و نیمی دیگر در یک قدمی سمت چپ می‌ایستند. دوباره همین کار را تکرار می‌کنیم. یک کودک که در سمت راست (در نقطه 1) ایستاده، به احتمال 50 درصد یک قدم دیگر به سمت راست می‌رود و در نقطه شماره 2 قرار می‌گیرد، یا یک قدم به چپ (همان‌جایی که در ابتدای بازی ایستاده بود) باز می‌گردد.

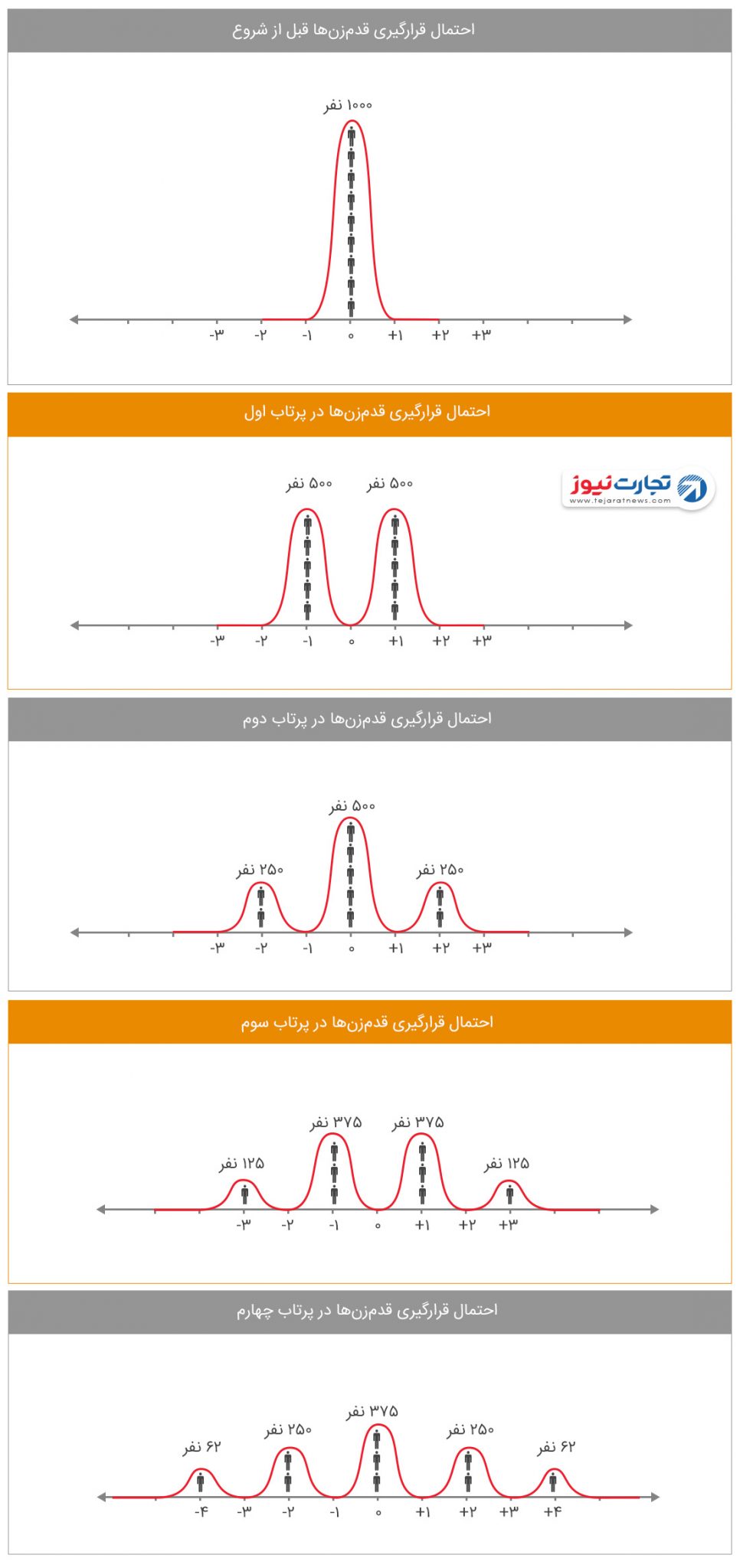
بعد از آن که برای هر کودک 2 بار سکه بیندازیم، نیمی از کودکان سمت راست و نیمی از کودکان سمت چپ به نقطه مبدا برمی‌گردند. یعنی 500 کودک در نقطه صفر خواهند بود. نیمی از 500 کودک (250 نفر) در نقطه 2+ و 250 کودک در نقطه 2- قرار می‌گیرند. طبیعی است که هیچ کودکی در نقطه 1+ یا 1- نباشد. چون (1+1)، (1-1)، (1+1-) و (1-1-) هرگز برابر 1± نمی‌شوند. توجه کنید که جهت جابجایی در مرحله دوم هیچ ارتباطی به جهت جابجایی مرحله اول ندارد.

می‌توانیم بازی را تا ابد ادامه بدهیم. مثلا اگر برای هر کودک 4 بار سکه بیندازیم به احتمال زیاد 375 کودک در مبدا، 250 کودک در نقطه 2± و 65 کودک در نقطه 4± باشند. قطعا هیچ کودکی در نقاط 1±، 3± و 5± نیست. هیچ کودکی هم نمی‌تواند در نقطه 6 و بالاتر باشد. چون با چهارقدم هرگز به آن نقطه نمی‌رسد.

رابطه ریاضی برای حرکت هر کودک

گفتیم بعد از چهاربار سکه انداختن احتمالا 65 کودک از 1000 کودک به نقطه 4 می‌رسند. اگر در ابتدای بازی بپرسید بعد از چهارمرحله «امیرکوچولوی ما» کجا می‌ایستد، نمی‌توانیم جوابی قطعی بدهیم. اما به شما توصیه می‌کنیم اول نقطه صفر را بررسی کنید، بعد به نقاط 2+ و 2- سر بزنید. اگر امیر خود را ملاقات نکردید او حتما در یکی از نقاط 4+ یا 4- است.

موقعیت هر کودک از جمع جبری هر حرکت او بدست می‌آید. مثلا فرض کنید فرزند شما 6 قدم برداشته است. اگر 4 قدم او به سمت راست و 2 قدم او به سمت چپ باشد، او در نقطه 2 ایستاده است. به بیان دیگر:

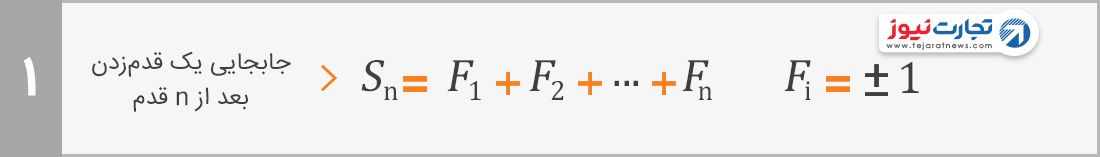
سوال اینجا است که به‌طور میانگین بچه‌ها در کجا خواهند ایستاد؟ مقدار میانگین محل قرارگیری بچه‌ها، برابر است با جمع میانگین هر حرکت او. چون میانگین (1 و 1-) برابر صفر است، میانگین حرکت بچه‌ها بعد از n قدم برابر می‌شود با n ضرب در صفر، یعنی صفر.

اگر بازی را تا همیشه ادامه دهیم، به یک توزیع زنگوله‌ای متقارن می‌رسیم. در این قدم‌زدن تصادفی همیشه بیشترین تعداد کودک در نقطه صفر یا در نقطه 1± می‌ایستند. نکته جالب این است که هر کودک ممکن است بارها و بارها به مبدا بازگردد. درست مثل مورچه‌ای که روی یک مداد راه برود و بارها و بارها از یک نقطه عبور کند.

قدم‌زدن نه‌چندان تصادفی

دیدیم که پرسه‌زدن تصادفی در عالم یک‌بعدی، بیشتر گشت‌وگذار در اطراف نقطه صفر است. یک مادر می‌تواند صندلی‌اش را آنجا بگذارد، کتاب بخواند و هر از گاهی زیر چشمی به فرزند دلبندش نگاه کند. اما چه می‌شود اگر یک بستنی‌فروشی در سمت راست بچه‌ها باشد؟ طبیعتا بچه‌ها بیش‌تر به سمت راست خواهند رفت.

در یک ولگشت جهت‌دار (Biased random walk) فرض کنید هر کودک به احتمال p به سمت راست و به احتمال 1-p به سمت چپ حرکت کند. اگر p=75% باشد به احتمال 75 درصد بچه به سمت راست و به احتمال 25 درصد بچه به سمت چپ می‌رود.

طبیعی است که بیش‌تر بچه‌ها کم‌کم به سمت راست حرکت کنند. احتمال جابجا شدن کودک برابر می‌شود با نیم قدم به سمت راست در هر مرحله (یا دو کودک به سمت راست یک کودک به سمت چپ):

اگر بازی تا n قدم دنبال شود، بیش‌تر بچه‌ها حول نقطه (n×(2p-1 قرار خواهند داشت. مثلا اگر p=50% باشد بیشتر بچه‌ها در اطراف نقطه صفر قرار می‌گیرند، اما برای p=75% محل تجمع بچه‌ها کم‌کم به سمت راست منتقل می‌شود. با این احتمال بعد از پرتاب 100 سکه برای هر کودک، بیش‌تر بچه‌ها حول نقطه 50 جمع شده‌اند.

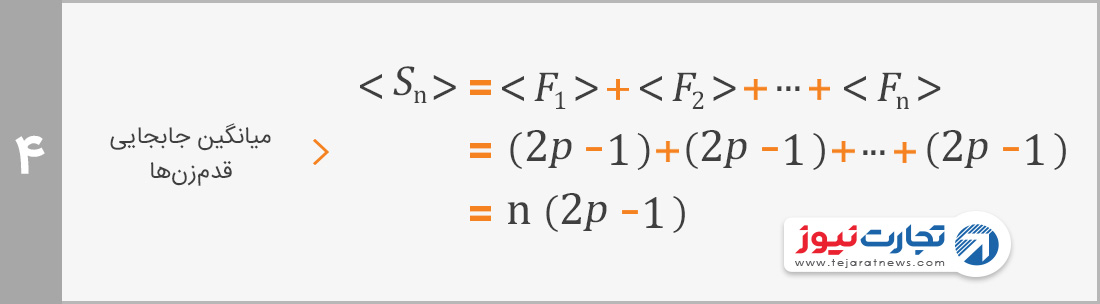
توجه به دونکته ضروری است. اول این که حرکت نقطه تعادل به سمت راست به این معنا نیست که هیچ کودکی نمی‌تواند به سمت چپ حرکت کند. در حالی که بیش‌تر بچه‌ها اطراف نقطه 50 هستند، امیرکوچولوی شما شاید در نقطه 100- باشد. دوم این که هنوز هم هیچ بچه‌ای نمی‌تواند از 100 و 100- فراتر رفته باشد.

قد‌مزدن تصادفی در یک صفحه کاغذ

تمام بحثی که تا اینجا داشتیم پرسه در طول یک خط صاف (فضای یک‌بعدی) بود. مهم‌ترین ویژگی در این ولگردی، بازگشت مداوم به نقطه آغاز و نوسان حول یک نقطه بود. نقطه‌ای که می‌توانست خود حرکت کند. بحث در دوبعد جالب‌تر می‌شود.

در یک قدم‌زدن تصادفی دوبعدی ، ذره می‌تواند به سمت راست‌وچپ یا بالا‌وپایین حرکت کند. مثل حالت یک‌بعدی باز هم بیشتر حرکت حول مبدا خواهد بود. همچنین احتمال حرکت به یک سمت 50% باشد، گردشگر تصادفی می‌تواند بارها از مبدا عبور کند.

اثر انگشت یک نمونه از قدم‌زدن تصادفی در صفحه دوبعدی است.

در فضای دوبعدی، این‌بار بجای آن‌که بگوییم کودکان به احتمال زیاد بر روی یک نقطه قرار می‌گیرند، باید از احتمال حضور آن‌ها بر روی دایره‌های متحدالمرکز حرف بزنیم. در یک پرسه تصادفی با احتمالِ حرکت 50%، بیش‌تر بچه‌ها در اطراف مرکز جمع می‌شوند. در حالی که با احتمال نامتقارن، مرکز تجمع حرکت می‌کند. بیش‌تر بچه‌ها حول این نقطه نوسان خواهند کرد.

بار دیگر باید تاکید کنیم که رفتار یک کودک می‌تواند کاتوره‌ای باشد. مثلا مسیر انتشار کپک روی نان، ساییدگی شلوار جین و حرکت کودکان در پارک از الگوی قدم‌زدن تصادفی دوبعدی پیروی می‌کند. (بچه‌ها پرواز نمی‌کنند.) بر روی یک نان، تمام کپک‌ها در یک نقطه مرکزی رها نشده‌اند. بلکه یک سلول در مسیری تصادفی تکثیر شده است. برای همین الگوی انتشار دایره‌ای نیست.

پرواز برفراز آشیانه فاخته

آخرین مرحله قابل تصور یک قدم‌زدن تصادفی در فضایی سه‌بعدی است. در فضای سه‌بعدی (و بیشتر) خیلی از قواعد ولگردی تغییر می‌کند. این حالت برای ما مهم است چون بیشتر اشیای واقعی (از جمله سهام) در دنیاهایی یک یا دوبعدی نیستند.

در فضای سه‌بعدی احتمال دارد گردشکر تصادفی هرگز به نقطه مبدا بازنگردد. یعنی ممکن است گردشگر خانه خود را ترک کند و هرگز دیگر به جای اول بازنگردد. از طرف دیگر خیلی بعید (تقریبا محال) است که یک قدم‌زن تصادفی دوبار از یک مسیر عبور کند. چون تصمیم‌های هر لحظه ارتباطی با تصمیم قبلی ندارد.

در اینجا هم امکان دارد که یک قدم‌زن به سمتی خاص کشیده شود. مثلا اگر احتمال بالا‌رفتن کمی بیشتر از احتمال پایین آمدن باشد، نوسانگر کم‌کم به سمت بالا جذب می‌شود.

پخش‌شدن جوهر در آب، انتشار دود و واکنش‌های هسته‌ای از این الگوی تصادفی پیروی می‌کنند. در هر حالت احتمال انتشار یک ذره در آب عدد مشخصی است، اما مولفه‌های راستای انتشار کاملا تصادفی هستند. محال است که جوهر پخش شده در آب دوباره در یک نقطه جمع شود و یک قطره تشکیل بدهد.

من مست و تو دیوانه

تمام ولگردهایی که تا این‌جا دیدیم با احتمالی ثابت به سمتی تصادفی کشیده می‌شدند. چه اتفاقی می‌افتد اگر احتمال انتشار هم از یک الگوی تصادفی پیروی کند؟

در این حالت یک قدم‌زن با احتمال p x به سمت راست و با احتمال p x -1 به سمت چپ حرکت می‌کند. اما p x عددی ثابت نیست و مدام تغییر می‌کند. اعداد تصادفی و متغیر p y و p z احتمال حرکت به جلووعقب و بالاوپایین را تعیین می‌کنند.

دود به عنوان یک قدم‌زن سه‌بعدی هرگز به نقطه اول باز نمی‌گردد.

با تصادفی شدن احتمال رفتارهای تصادفی، هر رفتار جدید به‌طور کامل از رفتار قبلی متمایز خواهد شد. کسی که الان پنج قدم به سمت راست رفته، در مرحله بعدی 50 قدم به چپ می‌آید و بعد بالا می‌رود.

اگر تعداد زیادی ولگرد از این الگوی تصادفیِ تصادفی پیروی کنند، بجای ایجاد شدن یک موج پیش‌رونده رفتاری آشوبناک به‌وجود خواهد آمد. در این حالت، این که اعداد تصادفی با چه الگوریتمی تولید شوند به شکل شانسی انتخاب شده و برای هر عدد تغییر می‌کند. مطالعه این مورد آشوبناک به هیچ‌عنوان کار راحتی نیست.

قدم‌زدن تصادفی در تالار شیشه‌ای

تمام ولگردها و پرسه‌زن‌های واقعی چنین رفتار پیچیده‌ای دارند. وقتی شما پشت کامپیوتر می‌نشینید، این که سهمی را بخرید یا بفروشید، این‌که چه حجمی بخرید یا بفروشید، این که با چه قیمتی بخرید یا بفروشید، این که در چه زمانی خرید یا فروش خود را ثبت کنید، این که بعد از خرید چقدر سهم را نگه‌دارید یا بعد از فروش کی دوباره همان نماد را بخرید، این که بعد از معامله یک سهم چه سهمی را معامله کنید و هزار متغیر دیگر، الگوریتیمی تصادفی دارد.

از یک طرف این الگوهای تصادفی مستقل از رفتار دیگر کنشگرهای بازار است و از طرف دیگر هر رفتار (با یک رابطه غیرخطی) با رفتار تعدادی تصادفی کنشگر جفت شده است. مثلا ممکن است اگر 20 نفر شروع به خرید یک سهم کنند، شما هم خرید کنید (با رشد قیمت سهم خود بفروشید). شاید با بالارفتن قیمت به فکر خرید بیفتید. این 20 نفر شاید باهم تبانی کرده باشند و شاید به طور تصادفی رفتاری مشابه کرده باشند. این که چندنفر به رفتار 20 نفرِ اول واکنش (مثبت یا منفی) نشان دهند، خود یک عدد تصادفی است.

فریب‌خورده در دنیایی تصادفی

وقتی به گذشته نگاه می‌کنیم، تمام اتفاق‌هایی که افتاده‌اند بدیهی به نظر می‌رسند. مثلا فکر کنید بار دیگر به سال 1384 بازگردیم، وقتی محمود احمدی‌نژاد رئیس‌جمهور ایران شد. به نظر بدیهی می‌آید که قیمت ارز و سکه جهشی انفجاری داشته باشد. اگر به سال 92 و پیروزی روحانی بازگردیم، واضح به‌نظر می‌رسد که بورس رشدی تاریخی تجربه کند.

اما الان در مورد آینده چه فکری می‌کنید؟ وضعیت بورس 1400 را چطور می‌بینید؟ بعضی‌ها سریع دیدگاه‌هایی منفی ارائه می‌کنند. چون منفی‌بافی امن است. اگر همه چیز بد شد شما درست گفته‌اید، اگر همه‌چیز خوب شد کسی از شما ناراحت نمی‌شود. اما واقعا چرا گذشته بدیهی است و آینده و مبهم؟ شاید چون مغز منطقی ما می‌کوشد برای رخدادهای تصادفی توجیه بتراشد. شاید رشد سال 92 فقط یک رخداد تصادفی بود که بر رخدادهای تصادفی دیگر اثر گذاشت. حالا ذهن ما برای این رخداد داستان می‌سازد. بعد خود را سرزنش می‌کنیم که «چرا سال 1392 تمام پول‌مان را نگذاشتیم در بورس؟»